第二回:『セットベースデザイン』ポイントベース設計とセットベース設計

セットベースデザインを「科学、シミュレーション、設計」の三回シリーズで解説します。
第二回では、ポイントベース設計の限界と多目的最適化の課題を整理し、性能・変数を範囲で扱う選好度セットベース設計を紹介。揺らぎや不確実性を前提とし、複数目標を同時に満足する新しい設計アプローチを解説します。
1.設計における不確実性
まず設計において対峙しなければならない不確実性について述べます。表題のそれぞれの設計に共通に関わるからです。
1.1.ポイント解であるが故の不確実性
最初に、ポイントベースの近似解析であるシミュレーション自体における不確実性について述べます。シミュレーションは設計の基本的道具として多用されています(ポイントベース設計)。多数の特定の性能について、求める時間(工数)を問題にしなければ、1回の計算で一つのモデルの性能状態をかなりの精度で求めることが可能です。しかしそこにはポイント解であるが故に、次のように注意を払うべき不確実性もあります。
a)シミュレーション性能を場の現象として考えた場合、「連続場の滑らかさ」や「全体場の連関」が直接的には無保証になること。つまり全体場現象の本質の表現ではなく、本質的には再現性を持たない、あるいは設計の反証性も保証されないフィツテイング(「予測」ではなく、「説明」)になる可能性が有り得ます。(応力集中や局所座屈の見落としなど)
b) 与えたモデル(境界条件・材料定数・形状・寸法)への依存性があります。ポイントベース解析は、固定値を入力して結果を得る仕組みです。現実の設計における荷重・温度・摩耗(接触)などの境界条件の難知性・不確実性への脆弱さ(それらの揺らぎ対策が難しい点)からくる不確実性があります。このモデルの依存性の課題は本質的であり、かつ現実的です。またそうして得た解析結果は「1点の代表解」であり、分布や信頼区間を表せないことになります。
c) 設計者の思考が「点依存」になることです。設計段階で「どの点でOKか」だけを見てしまい、設計全体のトレンド・系統設計・機構全体の因果関係を見失う可能性があり得ます。
1.2.設計行為の前提に関する不確実性
ポイントベースとセットベースの手法(内容は後述)によらず、設計行為自体の前提に伴う不確実性について述べます。つまり設計者が設計にあたって、状況に依っては確定的に設計を進められない外的要因(設計項目、その実現のための評価手法や影響因子などを内的要因といった際の、いわばそれらの外側にあって内的要因に影響を与える要因)としての不確実性です。いわば設計現場の環境的側面からくる不確実性です。具体的には、
a)設計者による確定が困難な状況(状況未確定、不確実な知識、正確な要求仕様決定の難しさなど)
b)他部門等からの影響や設計方針の変更(すり合わせの難しさ、他の設計者の意思決定の変動、企画やデザインの変動、製品の販売サイドの要望など)
c)ユーザの嗜好性の変動など
以上のような項目と内容があげられます。いずれも眼前にある直接的設計課題からみれば外的要因ともいうべき状況になります。ここではそれぞれについては項目をあげるだけに留めておきます。
2.ポイントベース設計とは
本稿の第一回に書きましたように、空間的にも時間的にも常に変化する連続現象の規則性を表現する支配方程式を微分方程式として表現し、これを現実の環境下(境界条件を含む設計課題)で解ける形(有限個の代数方程式)に再構築した結果の離散値(ポイント値)としての近似解をベースにし、計算機での処理を可能にした設計のことをいいます。つまり、無限次元空間の有限次元部分空間への射影という離散化を行っていることになります。近年、この解法は多くの物理現象への適用性が拡張していて、それをシミュレーションという意味合いで行う設計(CAE)は離散値をベースにしているが故にポイントベース設計そのものになります。
ポイントベース設計は、最近の計算機力の強大化に伴って、その勢いが増している感があります。しかし、第一回でも指摘したように、
①解法自体の誤差
②連続空間を要素や格子で代替する際の個数の有限性
③境界条件の付与の不確実性
の課題があります。特に①、②の課題に対する計算機力の挑戦は目を見張るものがあります。しかし逆に、その計算機力を体現したソフトの高騰化がユーザを限定化しているのも事実です。
以上は、一つの物理現象(あるいは連成化した物理現象も含めて)ごとにポイントベース化して解くときの課題ですが、設計側の課題としてみた場合には、背反性を伴うことも有る設計対象物理現象の複数化や非物理的事象(例えば、コスト、環境対応性、使用性など)の設計対象化といった多目的設計の課題もあります。一般には多目的最適化設計といわれる分野です。
2.1.ポイントベースによる多目的最適化
複数の背反する目的関数を持つ設計問題において、ある目的関数を改善しようとすると、他の少なくとも一つの目的関数が悪化してしまう(トレードオフ関係)ような解のことをパレート解といいます。これらの解は複数存在しその集合はパレートフロント(図1の赤線)といいます。
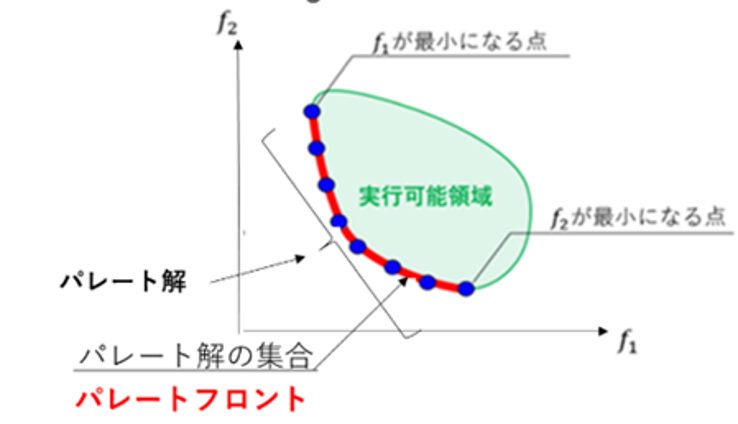
さらに、得られたパレートフロントからどの値の組合せを用いるかは別途の考え方(例えば、パラレルコーデイネートなど)が必要になります。2目的関数の最適化でも、一般にはきわめて多くの繰返しポイント計算が必要とされていて、必要な工数は少なくないといわれています。
この種のポイントベースで最適化を行う場合の目的数は4程度が限界ではないか、といわれています。一般に、5程度以上の目的数になると、パレート集合が高次元空間に広がり、同じ精度で探索するためには多くのサンプル数の指数的増加(サンプリングの爆発)が起こります。またほとんどの解が互いに支配関係を持たなくなり、すべてが“非劣解(Pareto optimal)”のように見えてしまいます。遺伝的アルゴリズム(GA)を用いて目的数4以上の場合に最適解を求める手法も検討されていますが、計算コストの急増が課題になります。
結果、目的数5程度以上の場合には原理的に可視化も困難であるだけでなく、局所最適への陥落も含めて最適化のアルゴリズムがどの方向へ探索すべきか分からなくなるといわれています。そもそも人間(設計者・意思決定者)が理解・評価できる認知目的数にも限界があります。つまり多目的最適解が得られたとしても、それが正当な解であることの理解が難しくなります。
その結果、結局、重みづけ(スカラー化)、制約条件化による簡略化に戻ることや不確実性定量化の分布推定を伴ったAI(機械学習)ベースのサロゲートモデル(ガウス過程回帰(統計モデル))、ニューラルネットワーク(AIモデル)、RBF(放射基底関数近似)など)の利用が検討されています。しかし、目的間の相関が高いと、サロゲートのモデル誤差も増幅されること、相関構造(共分散行列)が巨大化し、推定が不安定になること、不確実性定量化の分布推定(誤差の分布形や相関)の形が統一的に扱えなくなるなどという課題が生じることもあり得ます。
あるいは“好ましさ”をペアワイズ比較などで表現する補助的指標(選好モデル)を導入して、目的関数の重み付けをデータ駆動で推定し、望ましい領域を導く手法(PSBD)の提案もなされています。しかし本稿(第二回)では、次項以降に、設計変更や不確実性への対処の意味も込めて、性能と影響因子の両者に対して範囲と選好性を必須情報として与える選好モデルを出発点として、背反性を含む多目的性の全体満足性から多目的設計を行う選好度セットベース設計(PSD設計)について説明します。
3.選好度セットベース設計
ここまでにポイントベース計算(離散化計算)の科学としての成立性、ポイントベースを基礎にした設計におけるポイントであるが故の不確実性、設計現場の環境等から来る不確実性および多目的最適化における課題点などについて述べてきました。こうした不確実性や課題は、ある種、設計の対象・前提・側面における「(確率的)揺らぎ」や設計者側の思考やその表現の「点依存」性から来ていると思われます。
このように設計においては、前述の不確実性も含めて様々な「揺らぎ」が存在し、また設計者側の元来の思考は「点」で貫徹されたものではないことを考え合わせれば、「点」の代わりに、範囲(セット)で表現され、そこにおける傾向性(範囲内における現象の連続性)を基本にした設計の行為のほうが本来的であるし、人間の思考との親和性も自然であると考えられます。例えば、設計目標としての性能は「点」よりも、「~以上」、「~以下」、「この程度」といった範囲設定になることが一般的です。ここでは、ポイントベース設計での多目的最適化問題で生じている不確定性(揺らぎ)の処理やパレート解を求めるための計算回数の厖大化などの課題を克服するために、極端にいえば、性能や設計変数の範囲の両端情報のみで、それらを表現するセットベース設計手法について述べます。つまり、目的性能やそれらの影響因子(設計変数)の変化挙動に対して選好度概念を導入した範囲表現を用いて多目的性を同時実現する選好度セットベース設計手法について説明します。
3.1.選好度セットベース設計手法(1),(2)
提案されている選好度セットベース設計は、前述のようなまさにポイントベース設計におけるポイント(点)設計に影響を与える様々な不確実性、パレート最適化における目標数の制約、目標間の相関構造からくる課題、設計工数の厖大化などの問題点を克服するために、性能も影響因子もすべて範囲(セット)で表現し、範囲内の現象(変数)の連続性を基本として担保することから出発します。そのうえで設計上の多性能を同時に扱うことを前提とします。多性能であるが故に背反性を含むと同時に、範囲であるが故に各性能と影響因子に範囲の両端情報と範囲内選考性情報を与えて、全体としての満足性の高い多目的性能の同時実現範囲解を得る手法です。つまりすべての性能の目標範囲を同時満足する各性能の選好性の高い範囲(部分領域)とそれを実現する影響因子の範囲解を求める手法です。また各目標は背反性・両立性あるいは異種性の混在であり、それぞれの表現内容(現象)の単位は異なることが一般的ですが、それぞれの範囲目標に対する満足性を無次元化することで、上記の同時満足化を可能にしています。
以上述べた手法の概略を示したのが図2です。図の見方を以下に箇条書きします。
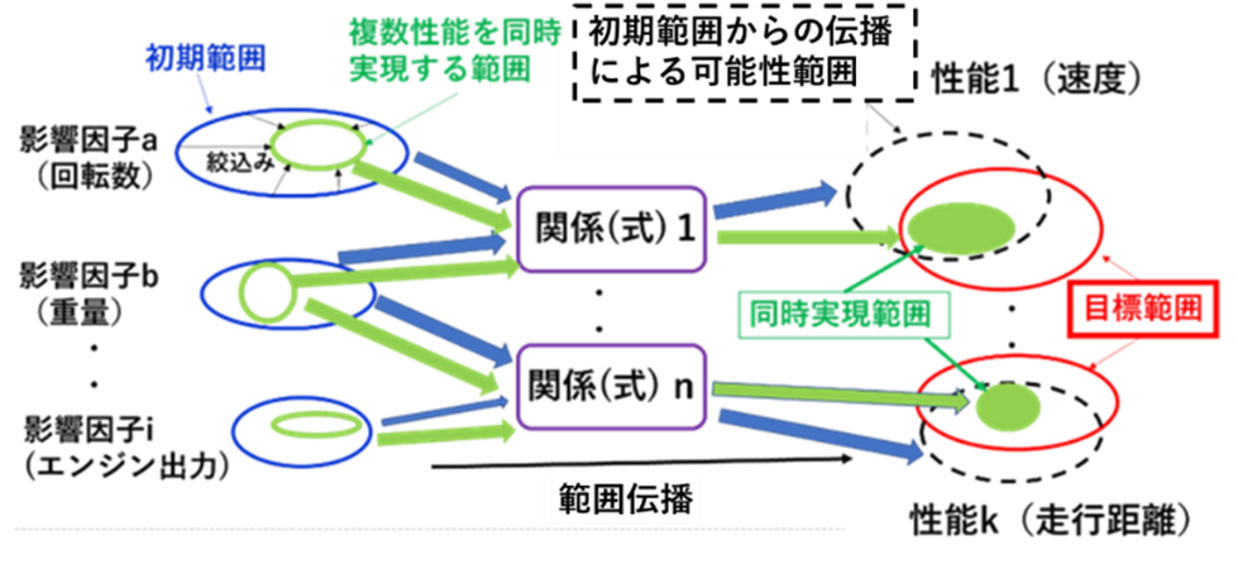
2)左側には、各性能に対する影響因子(a,b,・・,i)とその初期範囲(青楕円)を性能に対応するように示した。
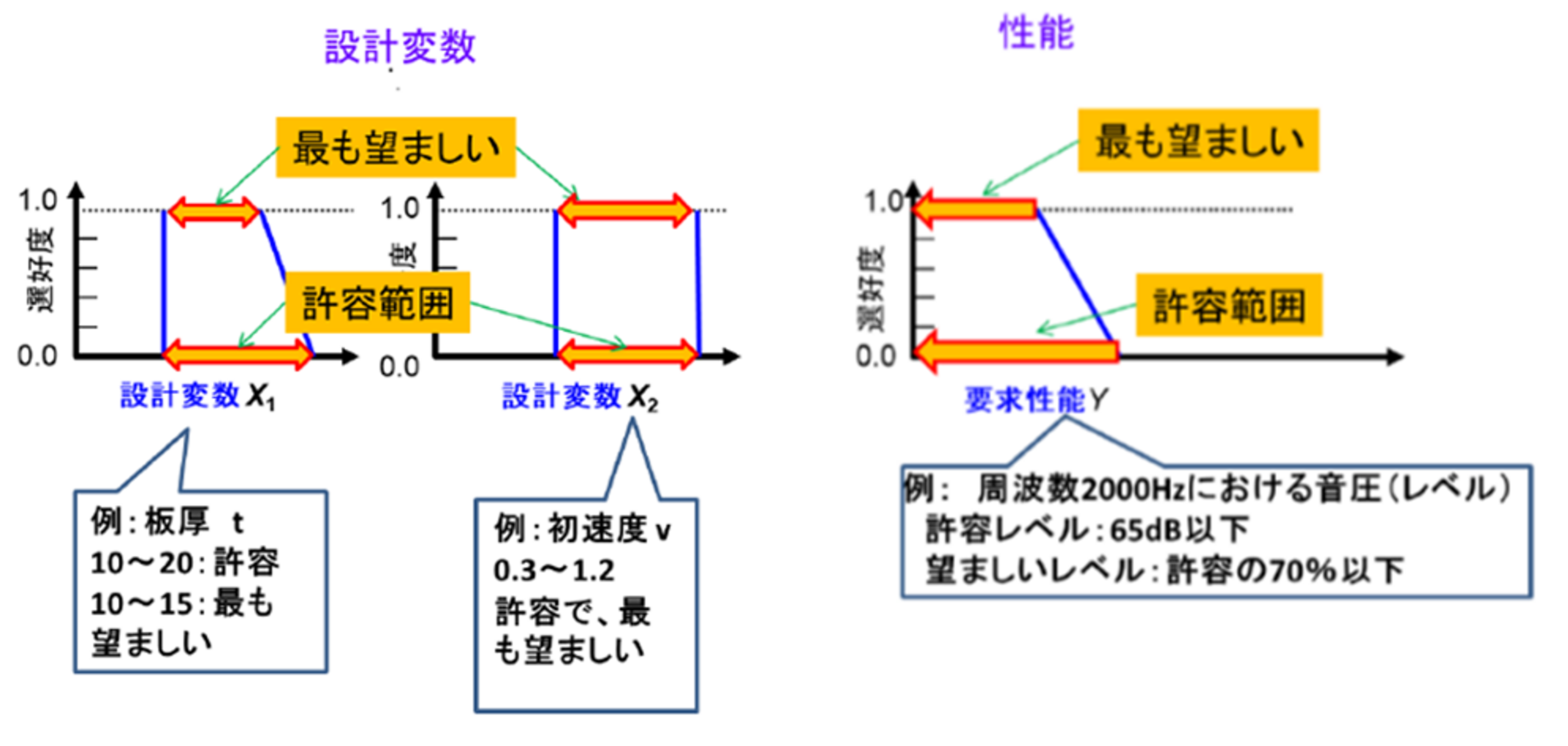
3)性能と影響因子の初期範囲には、選好度([0,1])の分布を与える。(図3参照)
4)中央には、各性能とそれぞれの影響因子(設計変数)との関係(式)を示した。具体的には、理論式(厳密式)、実験式、近似式(多項式、線形補間、放射基底関数など)、離散式(離散点を取る式)、機械学習関係、統計関係式(例えば、回帰分析式)などを用います。
5)影響因子の初期範囲を4)の関係(式)を用いて、各性能に範囲伝播(写像)します。その結果を示したのが右側の点線の楕円範囲(可能性範囲)になります。可能性範囲は各影響因子変数(範囲表現)の従属変数である性能f1(例えば、f1(x1,x2,・・xf))の範囲を集合演算で求めた結果です。この可能性範囲がそれぞれ目標範囲(赤楕円)にすべて入っていれば(緑の範囲)、左側の初期範囲はそのまま解範囲になります。なお、それぞれの範囲内では離散式を除いて演算可能な無限個の点の集合となっています。
6)一つの性能でも赤楕円範囲に入っていなければ、多目的性能の同時満足範囲解は無しとなります。
7)すべての性能が部分的にであっても赤範囲に入っていれば、左側の影響因子の初期範囲は解範囲を有しています。
8)その部分的解範囲をすべての性能範囲の同時満足という観点から求めるために、すべての影響因子の初期範囲を同一のアルゴリズムで絞込み(部分化)を行います。
9)部分化された各範囲を範囲伝播して得られる可能性範囲はその範囲の大きさと範囲の存在箇所における選好度分布に基づく積分的(範囲とそこにおける選好度分布の積分)評価、つまり満足度の評価を受けます。性能ごとの積分値(満足度)の全性能における平均がもっとも大きい分割範囲の組合せを解範囲として出力します。
文献
(1)南、石川、初期設計段階におけるセットベース多目的設計最適化(第1報)、自動車技術会36巻6号(2005)pp.157-162
(2)Y.-E. Nahm, H. Ishikawa, Novel space-based design methodology for preliminary engineering design, Int J Adv Manuf Technol, 28 (2006)pp.1056-1070.

最適化/機械学習による設計空間探索ソフトウエア pSeven Desktop
pSeven Desktopであらゆる設計リードタイムを短縮。煩わしい作業を削減し、CAD・CAE・データとプロセスを自動化します。pSeven Desktop独自のAIと強力な自動化エンジンによって、最適な設計条件を効率的に発見が可能です。

設計最適化と自動化を実現する革新的なエンタープライズ基盤 pSeven Enterprise
設計プロセスの自動化・最適化、モデル・ワークフローの統合と展開を目的としたエンタープライズ向けのデータ活用プラットフォームです。設計者やエンジニアが組織を横断し、複合領域の複雑な課題を解決するために、最適化技術、機械学習モデル・シミュレーションモデルの統合、ノーコードアプリの活用を支援します。
